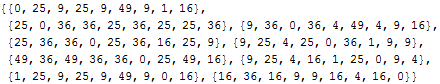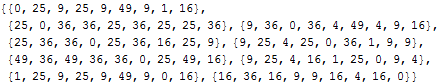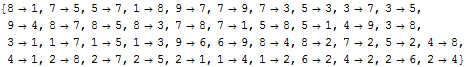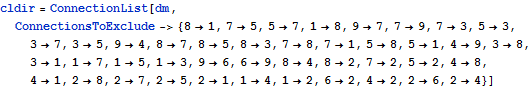Obtuse Angle Shadowing Networks
If you deal with experimental data in any form, it is a very common case that you can represent the data as a set of numbered scattered points in an abstract point space. You might have a lot of numerical information about the cloud of points, but to be able to gain knowledge, you should look for structures, patterns and relations in this cloud. You should look for outliers, for typical points and point neighborhoods, for shapes like threads, sheets and holes, etc. Suppose, that you have such a set of scattered points in any or an unknown number of dimensions, and that maybe you do not know their coordinates, but you know how to calculate the distance between them. To be able to learn anything about your diffuse cloud of points, it is very useful to have tools to categorize the relations between the points and the shape of the cloud. You can use the distance information to define an
obtuse-angle shadowing network connecting nearby points in the set. If you have a function defined on this point set, you might use this network to define a
distance-based interpolation function to estimate the function value for a new point of the same kind. Such networks and this kind of interpolation should have applications in various fields, for example image processing and machine learning. The Obtuse package provides
Mathematica functions to find and investigate such networks, and to use them for interpolation. This tutorial introduces the network routines. The tutorial
Scattered Point Interpolation treats the interpolation routines, together with some other interpolation methods.
The obtuse-angle shadowing rule
We want to find a rule that connects nearby points, but leave distant points unconnected. Here we introduce a shadowing rule for this task. The basic idea for the shadowing rule is that one point
C in the network might stop the point
A from being connected to
B, if there is a connection from
C to
B and if the angle
AC -
CB is strictly obtuse. Note, that no connection between
A and
C is required. Now we have to make this shadowing rule a little bit more complicated to sort out some ambiguous cases, and to differentiate between directed and undirected connections.
If the option
Type is set to Directed: The point A in the point set is NOT connected to the point B if there exist one other points C in the point set, such that C is connected to B and the angle ACB is obtuse. Further, two points in the network are NOT connected if the distance between them is smaller or equal to
SmoothenDistance or larger or equal to twice the
CutoffRadius.
If the option
Type is set to Undirected: Two points A and B in the point set are NOT connected if there exist two other points C and D (maybe identical) in the point set, such that C is connected to A and D is connected to B and both the angles ACB and ADB are obtuse. Further, two points in the network are NOT connected if the distance between them is smaller or equal to
SmoothenDistance or larger or equal to twice the
CutoffRadius. Each connected point pair occurs only once in the returned list, with the lowest point number coming first.
Obtaining a connection list from a distance matrix.
Calculate the distance matrix, using
DirectedDistanceMatrix
| Out[11]= | 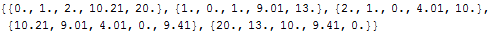 |
Use this distance matrix to calculate the connection list:
| Out[12]= | 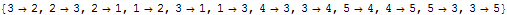 |
The points
pts does not need to be numerical data, they could also be Boolean data or string data. By setting the option
DistanceFunction to
DirectedDistanceMatrix, one can adapt the system to e.g. periodic boundary conditions.
Calculate the distance matrix, using the squared elements of the
DirectedDistanceMatrix. (It is a philosphical question here if one should use the distance matrix directly, or if it should be squared.)
| Out[14]= | 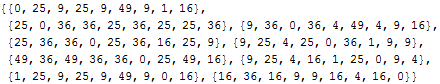 |
Here is an alternative way, using the option
DistanceFunction
| Out[15]= | 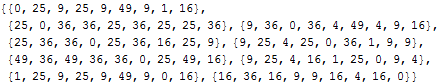 |
Use this distance matrix to calculate the connection list:
| Out[16]= | 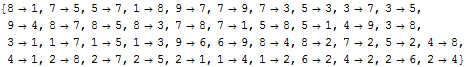 |
If we exclude all the connections here, using the option
ConnectionsToExclude, we get a second level of connections:
| Out[11]= | 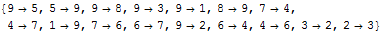 |
We can also use the option
NeighborLevel to obtain the same result:
| Out[33]= | 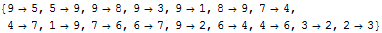 |
If we proceed with
NeighborLevel to higher numbers, we will exhaust all connections:
| Out[34]= | 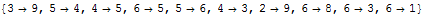 |
| Out[35]= | 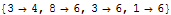 |
| Out[36]= |  |
Options for ConnectionList
More examples can be found in the help for
ConnectionList.
| | |
| DistanceFunction | Automatic | distance function to use in calculation of the distance matrix and the calculation of the distance from the interpolation point to the control points. Note, that the function here is expected to return the square of the distance. The distance function might be asymmeric |
Options for DirectedDistanceMatrix
| ConnectedFrom[j,conlist] | gives a list of numbers for those points which are connected from point number j according to the connection list conlist. |
| ConnectedTo[j,conlist] | gives a list of numbers for those points which are connected to point number j according to the connection list conlist. |
| ConnectedNeighbors[j,conlist] | gives a list of numbers for those points which are connected from or to point number j according to the connection list conlist. |
| FriendCountList[conlist] | sorts the points according to how many connections they have in conlist. |
| FriendsFromList[conlist] | sorts the points according to which points they have connections from and returns a list of list of numbers |
| FriendsList[conlist] | sorts the points according to which points they have connections from or to and returns a list of list of numbers |
| FriendsToList[conlist] | sorts the points according to which points they have connections to and returns a list of list of numbers |
Utilities for investigation of a connection list.
Example using the utility functions
The same 2D-points as above:
| Out[14]= | 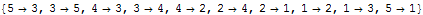 |
| Out[15]= | 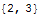 |
| Out[16]= | 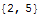 |
| Out[17]= | 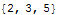 |
| Out[18]= | 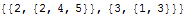 |
| Out[19]= | 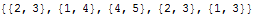 |
| Out[20]= | 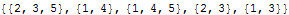 |
| Out[21]= | 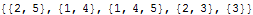 |